The Grand Coherence, Chapter 2: How to Decide What to Believe
This post is part of the book The Grand Coherence: A Modern Defense of Christianity. For all the links in the book, see this introductory post. To listen to this chapter, go to this link: Chapter 2.
You’ve probably noticed that people agree easily about a lot of things, but they disagree about religion.
As a few examples of easy agreement, you and I and the next stranger you see on the street could all agree that summer is hotter than winter, and that oak leaves fall in autumn, that cars can drive fast and the moon is white, that cats hunt mice and ticks bite people, that Isaac Newton discovered the law of gravity, that ice cream is cold and sweet, that 2+3=5, and that Bill Gates is rich. I could go on and on.
But colleagues in the same office, students in the same school, and even members of the same family disagree about whether God exists, whether miracles occur, whether Jesus was divine, whether there is a devil, whether it is right to read the Bible and obey its rules, and whether human beings can live forever.
Is religion unique? Aren’t there other things we disagree about? What about politics? That’s not the same. Political disagreement is usually about clashing preferences and values rather than facts. I may deplore a president whom my neighbor admires: we call that a “matter of opinion.” But we agree who is president: we call that a “fact.” By contrast, in religion we disagree, first of all, about facts. Does God exist? Did Jesus rise from the dead?
Disagreement about religion contrasts with easy agreement about many facts of everyday life. Yet there is an interesting group of people who have a long-standing professional hobby of dissenting from the easy, complacent agreement that most people share. They are called philosophers, and it is their distinguishing mark to question everything. As some people think that religion begins with a “leap of faith,” so philosophy begins with what might be called a leap of doubt.
In ancient times, the philosopher Socrates (470-399 BC) questioned everyone, and reduced them to confusion. They found themselves led into self-contradiction. When this practice annoyed the Athenians to the point of wanting to kill him, he explained, at his trial, that he knew nothing, yet an oracle had once told him that he was the wisest man in Greece! In asking questions, he had been trying to disprove the oracle by finding someone wiser than himself. Instead, he told the jury, he had inadvertently proved the oracle right in the end, for he discovered that no one else knew anything either, but he at least knew he knew nothing, which gave him some advantage. This defense made the Athenians so angry that they put Socrates to death. He has been a kind of secular patron saint of philosophy and critical thinking ever since. He was a martyr, not to faith, but to doubt.
Modern philosophy began rather similarly, when Rene Descartes (1596-1650) decided that all his beliefs were unfounded. He began to systematically demolish them, in order to rebuild his beliefs on truer foundations. He doubted so much that he was left with nothing but “I think therefore I am.” That was his only belief that he could not doubt, so it became the beginning of his philosophy. Descartes went on to argue that there must be a God to sustain things, and God, being perfect, would not be deceptive, so our commonplace beliefs are valid after all… but this part of Descartes’ argument has satisfied few, and philosophers since have generally imitated his question rather than his answer. It has become the lofty duty of philosophers to take Descartes’s leap of doubt.
The British empiricists Locke (1632-1704), Berkeley (1685-1753) and Hume (1711-1776) pursued the project of doubt still more resolutely than Descartes. David Hume carried critical inquiry so far as to call into question whether inductive reasoning itself, that is, the inference from patterns that is the basis of all science, is valid. Hume’s philosophy seems to lead to complete skepticism, that is, the abandonment of all our claims to know anything, a conclusion that is probably not psychologically possible to fully embrace. But Hume’s great leap of doubt also became part of the heritage of philosophy, and generations of philosophers have taken it. I myself took the leap of doubt long ago, somewhere around age 20, after being raised in a church that taught odd things, which intellectual honesty forced me to leave. Trying to figure things out on my own has been an interesting adventure, and it led me, in due course, to the truths I know today, so I’m grateful for the examples of Socrates, Descartes, Hume and other philosophers who served as role models for the leap of doubt that began my journey.
To this day, the abstract skeptic, who lies in wait at the end of the long road of critical inquiry, still haunts philosophers. They worry a good deal about how to refute the skeptic and prove that mankind is entitled to claim some knowledge. Ordinary people, meanwhile, are not troubled by the question. They take it for granted that people know things. The philosopher’s leap of doubt may seem silly, yet philosophy has accomplished a great deal by doubting away false inherited beliefs and opening the door to new, truer ones. From the doubts of Socrates sprang the genius of Plato (maybe 428-348 BC) and the practical wisdom of Aristotle (384-322 BC), and Descartes helped to set the stage for modern science.
But we can’t let doubt have everything its way. People of all cultures confidently believe lots of things in common, as they need to, and ought to. They believe, for example, that they have feet and knees and hands and chests, that words have meaning, that food is good for the body, that day alternates with night, that trees are green, roses are red, skies are blue, clouds are white, and far, far more. There is nothing wrong with asking how we know these things, if we can find a good answer. But to sacrifice these universal, necessary beliefs to our philosophical scruples would be a pitiful trap to fall into. How would a skeptic live for a single day? He couldn't even get out of bed in the morning, because infinite doubt would have erased from his mind the knowledge that the floor will bear his weight.
To avoid falling into the trap of infinite doubt, we need, first of all, to explain, and hopefully to more or less justify, people’s easy agreement about a vast variety of everyday, commonsense beliefs. And yet we need to do it without proving too much, for if we end up concluding that everyone must agree about everything, then our conclusion will be contradicted by, among other things, the vast disagreements that prevail among people when it comes to religion.
I think I know where to begin an explanation of everyday commonsense agreement about things. It’s called Bayes’ Law.
Bayes’ Law is a mathematical rule for how rational people should update their beliefs in response to new evidence. It states-- prepare to be confused!-- that the probability that theory A is true, given evidence B, is the product of the probability that evidence B would be observed, if A were true, times the prior odds that theory A is true, divided by the prior odds that event B would be observed. The prior odds that event B would be observed, in turn, are the odds that B would be observed if A is true times the probability that A is true, plus the odds that B would be observed if A is false, times the probability that A is false.
Here it is in mathematical notation:
PA|B=PB|APAPB|AP(A)+P(B|-A)P(-A)
What is hard in the abstract often becomes easy in an example.
Suppose a famous jewel is stolen from a duke’s treasury, and the suspects are master burglar Dapper Dick and amateur burglar Slick Stan. A detective investigating the case initially thinks the odds are 95% that the thief was Dapper Dick. He then learns that Slick Stan was seen prowling in an out-of-the-way village very near the castle from which the jewel was stolen, just a few hours before the theft. How likely is it now that Slick Stan is the culprit?
To settle that using Bayes’ Law, the detective must first settle:
P(A), the prior likelihood that Slick Stan is the thief, which is 5%.
P(B|A), the likelihood that Slick Stan would have been in that village, if he were on his way to the crime. Let’s say that’s 20%.
P(B|-A), the likelihood that Slick Stan would have been in that village, without being on his way to the crime. Let’s say that’s 1%.
Bayes’ Law then yields:
PA|B=PB|APAPB|AP(A)+P(B|-A)P(-A)=20%×5%20%×5%+1%×95%=51.3%
A 51% probability of guilt isn’t enough to convict, but the sighting of Slick Stan near the scene of the crime makes him, narrowly, the prime suspect. So, with the help of Bayes’ Law, a clue has been put to good use.
Now, I may seem to have used a lot of words and difficult symbols to make a very simple point. Anyone could have figured out, without help from Bayes’ Law, that it was suspicious that Slick Stan was lurking so near the scene of the crime, and the lack of an innocent reason for him to have been there strongly suggests that he stole the jewel.
What the math does here is to codify common sense. And turning commonsense, intuitive reasoning into math, though it seems laborious and pedantic at first, has its benefits. It provides a hard logical warrant for what might otherwise seem like just a feeling. It helps us generalize from situations we readily understand to situations that are more confusing. And it reveals an important and subtle truth, namely, that our ability to process evidence is dependent on many background beliefs that comprise our worldview.
In order to process and draw a conclusion from a piece of evidence, the detective needed three prior beliefs, one about Slick Stan’s guilt, and two beliefs about his likelihood of visiting the village with or without a criminal errand in the vicinity. What justification does he have for those prior beliefs? Perhaps they, in their turn, had Bayesian justifications, but if so, that would require even more priors. The chain of Bayesian inference keeps branching more and more, without any terminus. The arbitrariness of priors cannot be overcome.
This may seem like a very damaging objection to Bayes’ Law as a principle for practical reasoning. But it turns out that new evidence always moves good Bayesian rationalists in the same direction. So as evidence accumulates, they converge on the truth.
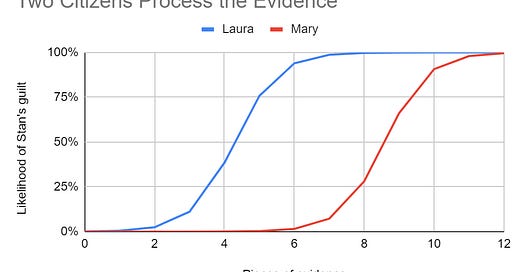
An example may illustrate the point. Suppose there are two citizens living near the castle, Laura and Mary, who hear about the jewel theft. Both of them initially disbelieve the allegation that Slick Stan was the thief. Laura thinks there’s only one chance in a thousand that Stan stole the diamond. Mary thinks there’s only one chance in a million. But then more and more bits of evidence appear, which, though none of them are conclusive in themselves, are all more consistent with Stan’s guilt than his innocence. The chart below shows what happens to these two subjects as the evidence accumulates. (I can provide the spreadsheet with the calculations behind the chart to anyone who is interested.)
This chart offers three big lessons:
People converge on the truth, if there’s enough evidence.
People tend to change their minds fairly quickly if they do it at all, because intermediate states of confidence are unstable.
Extreme disagreement can be rational when there is a middling amount of evidence.
The first lesson is intuitive and reassuring. Evidence persuades. Data changes minds. As more and more relevant information accumulates, people’s views come increasingly into agreement with each other. We sought an explanation for why people agree on such a vast variety of everyday, commonsense beliefs to live by. Now we’ve found one. All people need to do is process evidence in roughly Bayesian fashion, and they can learn from experience and converge on the truth. So far, so good.
The second lesson is more surprising. Laura and Mary change their minds at different times, but when the change comes, it happens fairly quickly. The movement in their states of belief is very non-linear. It’s very slow at first, then fast, then slow again. When they are almost sure that Stan is innocent, or guilty, a bit more evidence doesn’t move them very much. Confident beliefs are stable. But when they are very uncertain, every bit of evidence matters a lot. Doubt is unstable. Does your experience confirm this? I think mine does. Religious conversions, in particular, don’t usually happen overnight, but often occur over the course of a couple of years or even a few months, which is a short time in the grand scheme of things.
The third lesson is so counter-intuitive that I would find it hard to believe if I hadn't just proved it with math. When two people confidently hold opposite opinions, we might assume that either they’ve seen very different evidence, or that at least one of them is not being very rational. But Laura and Mary, after seeing the exact same six pieces of evidence, diametrically disagree, even though they are perfect Bayesian rationalists. Why? Because they had different priors. Yet the difference in their priors was so slight that it could scarcely have been discerned. Both might have said they were sure that Stan was innocent. There was a difference, but it seems meaningless. And yet new evidence drove an enormous wedge between people who initially agreed. Does experience confirm this? It's hard to come up with clear examples of it, yet one does stand out: the Resurrection of Jesus. We’ll do math on that one in the next chapter, but it’s clearly a claim about which smart people diametrically disagree, even when they seem to have all the same evidence available to them.
So why do we agree? What is the explanation of everyday commonsense agreement about things?
Let's start with this story, though we may need to revise it later: Ordinary commonsense knowledge is explained and justified by the way we learn from experience. There are rules of evidence that we apply instinctively, but that can be logically grounded in Bayes’ Law. We are always watching, listening, swapping stories, and thinking. As we do this, our general notions about the world, wherever they come from-- and usually, we can’t remember that-- are constantly being tested by experience. Most of the time, these general notions put us at our ease, and make the world predictable. When the world meets our expectations, we invest still more confidence in the general notions that successfully predicted how things would go.
Sometimes, events take us by surprise, and we have to deal with the unexpected. When that happens, we revisit the general notions that gave us the false expectations, and doubt or discard them. In adults, this process has been going on for many years, and by learning from experience, we have acquired a worldview, which is not infallibly right, but is fairly accurate with respect to the bits of the world that we customarily inhabit, and the situations in which we find ourselves every day. Others have learned in the same way, so their worldview is largely the same as ours, in these sorts of ordinary situations.
Of course, we can’t remember the learning process. We can’t remember all the evidence we’ve seen. We can’t remember all the times when one of our general notions was reinforced, or corrected, or forgotten. The full tale of all our experiences is lost, or remembered only by God. But we know more or less how our minds work. And so, looking backward, we can guess, more or less, how our notions came to be what they are. When Bayes’ Law shows us how, logically, evidence ought to be processed, we can recognize that that’s what we habitually do, or close to it. Therefore, we have reason to think that our worldviews are reliable.
Since we can see that other people process evidence similarly to the way we process it ourselves, we can regard their worldviews as more or less reliable, too. Learning from others is quite consistent with Bayesian rationality. An opinion held by another is a bit of evidence that that opinion is true. In this way, individual minds meld together somewhat, forming a culture, and a lot of beliefs are borrowed from the culture, all quite rationally. We use words like “common sense” or “common knowledge” to describe beliefs that are generally shared in this way.
Again, this account of the basis of knowledge will need some objection handling and refinement later on, but it will do for now. The other part of the challenge was to avoid proving too much by leaving room in our account of knowledge for persistent religious disagreement. Have we succeeded in that too? Why is religion different?
There are three answers.
First, religion often deals in matters where the data is especially scanty. It deals in what is rare, exceptional and wonderful. It deals in what lies at the edges of experience. Pagans didn’t generally claim to have seen Zeus or Apollo, yet there were tales that mortals had sometimes been visited by the gods and seen them face to face. Consider the example of lightning, which has sometimes gotten a special religious explanation. Everyone in pagan times, as today, had seen it. No one had actually seen Zeus or Thor wield it. But they wouldn’t expect to, since they couldn’t get up in the thunderclouds to see what was happening. Without data, there was no way to refute the tale that lightning was a god’s weapon. When Christians tell tales of miracles, likewise, the data to support the tales is sometimes a bit scanty. And where do we go after we die? The dead tell no tales, so we have little evidence, and absent revelation, fancies and guesswork have the field to themselves.
Second, religious disagreements may be semantic rather than substantive. For example, some say they believe in God, some that they don't, some that they aren't sure. But people's external policy of representing themselves as believing in God, or not, may not correlate very well with their inner state of belief. People can mean a lot of different things by the word “God,” and some who say there is no God may be denying one conception of God, while being ready to accept another. A man brought up to believe in an angry fire-and-brimstone “God” who comes to disbelieve in that, while still feeling that there is some foundation of being, some source of meaning, some transcendent principle, for which he feels reverence, might say “I believe in God, but…” or “I don’t believe in God, but…” and mean the same thing. In ancient times, some pagans worshipped “Zeus” and others “Jupiter,” until it was settled that Zeus and Jupiter were the same god, but were they, really? What would that even mean? Religious language can be cryptic, vague, opaque, and metaphysically challenging. It has to be, because it deals with things so subtle and interior and transcendent, but the consequence is that religious language leaves much room for interpretation and misunderstanding. Sometimes a clash of words is not a clash of ideas. Sometimes we can’t tell.
But third, there is one religious disagreement which is not at all semantic, and does not arise from a lack of evidence. Did Jesus rise from the dead, or not? It is strictly a question of fact, the sort of well-defined practical fact that hard-nosed, no-nonsense journalists would write about, and police and courts would try to settle. A man in Palestine, long ago but still in the midst of recorded history, was killed, very publicly, and seen by many thoroughly dead, and then, shortly afterwards, was seen again, this time alive, by many people. This claim poses no metaphysical difficulties. We know what it is to be alive, and to be dead. It is a surprising claim, because people usually go only from living to dead and not the other way, but the evidence for it would be sufficient to establish any less extraordinary claim. What are we to make of it?
It’s a good opportunity to put Bayes’ Law to work.